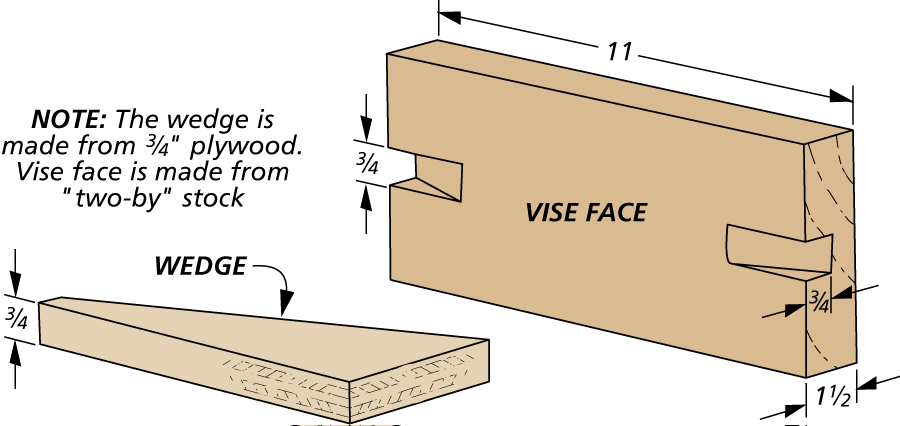
MARCENARIA POCKET HOLE
Se você gosta de marcenaria ou faz projetos em casa, inevitavelmente precisará prender duas peças de madeira uma na outra. Existem muitas maneiras de juntar madeira - as opções podem variar de cola a pregos e marcenaria complexa. Cada um oferece vantagens e desvantagens em termos de força, velocidade, facilidade de uso, habilidades e requisitos de ferramenta.
Vamos nos concentrar em uma maneira de criar juntas fortes e de qualidade profissional: orifícios de bolso. Os fabricantes de móveis profissionais usam a marcenaria de orifícios de bolso há anos. E por uma boa razão - é uma maneira simples de conseguir uma união forte e permanente de duas peças de madeira. Mas a marcenaria pocket hole não é apenas para marcenaria. É um dos melhores métodos para unir duas peças de madeira em que uma junta forte, sem fechos visíveis em uma superfície, é a ordem do dia.
Então, o que é exatamente um buraco de bolso? É simplesmente um orifício feito em um ângulo que forma uma “bolsa” para o parafuso ser inserido. O que o faz funcionar é o design do gabarito. Ele orienta a broca na madeira em um ângulo preciso para produzir um orifício cuidadosamente projetado para alojar a cabeça do parafuso. Depois que o buraco da bolsa é perfurado, um parafuso cementado especialmente projetado com uma ponta autoperfurante é usado. Os parafusos seguram-se com firmeza e não partem a madeira, mesmo em madeiras nobres.
Vantagens:
Articulações confiáveis e fortes.
Rápido - sem cortes exatos e complicados. Basta fazer os orifícios do bolso, alinhar suas peças e colocar os parafusos no lugar.
Forte - os parafusos auto-roscantes exercem uma enorme pressão de aperto e os parafusos permanecem na peça permanentemente; é como ser capaz de deixar seu projeto firmemente preso - para sempre.
Cada junta é montada separadamente, portanto, você só precisa usar uma braçadeira para concluir um projeto.
Sem espera! Não há necessidade de esperar que a cola seque antes de continuar com seu projeto. Depois de apertar os parafusos, a junta é montada permanentemente.
Existem muitos usos para juntas de orifício de bolso: armários, junção de borda (sem grampos de barra), mesas, cadeiras, porta-retratos, escadas, decks, rebordo de bancada e muito mais. Já tentou prender uma curva? A marcenaria de orifícios facilita a montagem de peças com ângulos irregulares e confere rigidez extra às formas curvas.
Se o seu projeto envolver a união de duas peças de madeira, considere a marcenaria de orifício de bolso. Depois de perceber como a marcenaria de orifício de bolso é rápida, forte e simples, você se perguntará como conseguiu viver sem ela!
É fácil! Furar. Dirigir. Feito.
Tradução do Blog
Original em inglês: https://www.woodcraft.com/blog_entries/pocket-hole-joinery?tag=Joinery
não deu para melhorar e deixar mais clara a imagem
http://www.greensawdiy.com/pocket-hole-jig-making-diy.html
Friedrich Wilhelm Nietzsche foi um filósofo, filólogo, crítico cultural, poeta e compositor prussiano do século XIX, nascido na atual Alemanha. Escreveu vários textos criticando a religião, a moral, a cultura contemporânea, filosofia e ciência, exibindo uma predileção por metáfora, ironia e aforismo. Wikipédia
Nascimento: 15 de outubro de 1844, Röcken, Lützen, Alemanha
Falecimento: 25 de agosto de 1900, Weimar, Alemanha
Formação: Universidade de Leipzig (1865–1869),
Irmãos: Elisabeth Förster-Nietzsche, Ludwig Joseph Nietzsche
Pais: Carl Ludwig Nietzsche, Franziska Oehler
Saiba mais em: https://pt.wikipedia.org/wiki/Friedrich_Nietzsche